MindLLM and Neuroscience-Informed Attention: Decoding the Brain with Language Models
MindLLM and Neuroscience-Informed Attention: Decoding the Brain with Language Models
MindLLM represents a significant advancement in brain decoding. It combines neuroscience-driven design with powerful language models to generate natural language from fMRI brain activity.
This post unpacks the neuroscience-informed attention at the heart of MindLLM, and includes a step-by-step code example.
🧭 Visual Walkthrough
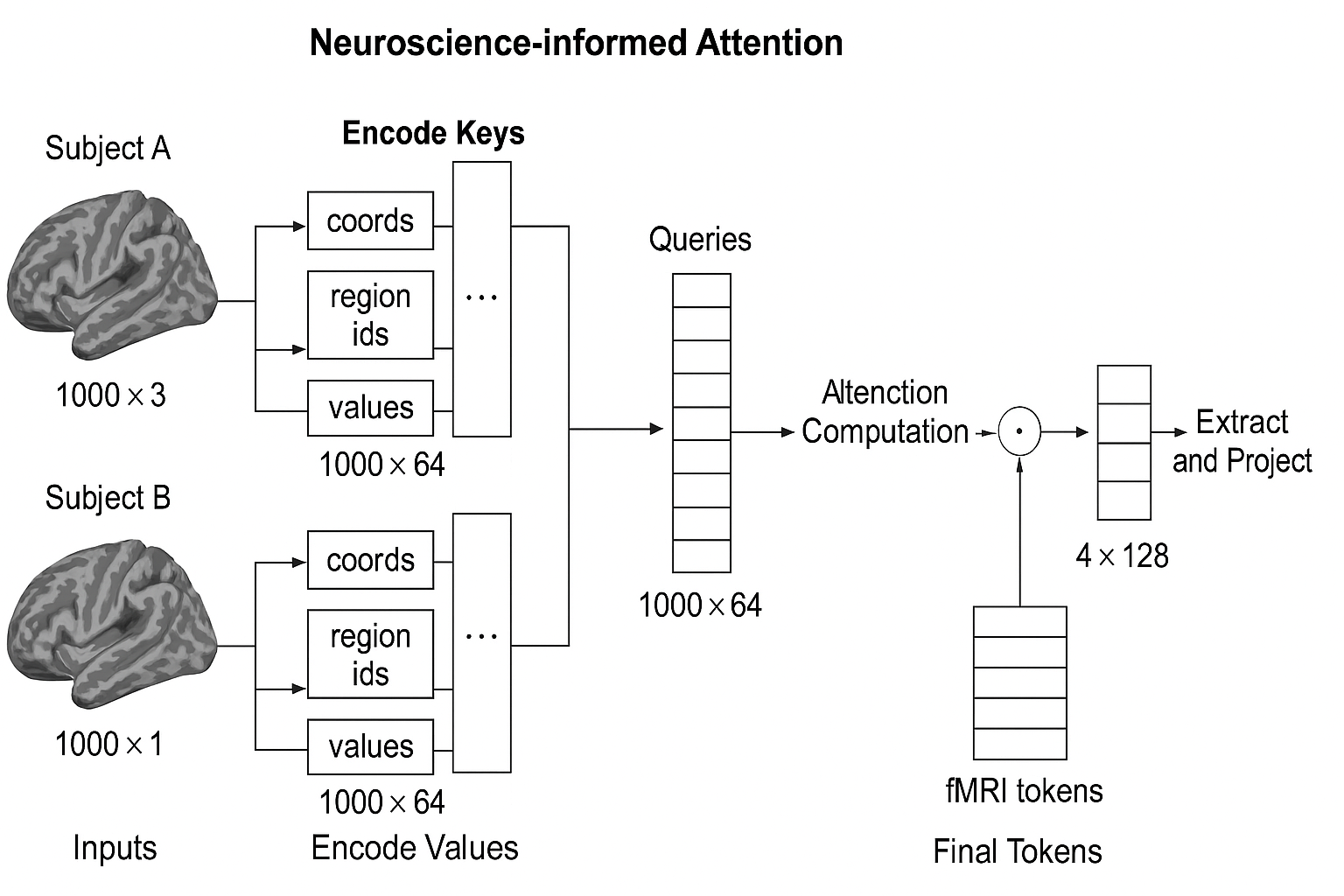
The diagram below illustrates the full neuroscience-informed attention pipeline for two subjects with different fMRI voxel sets:
📥 Download the Slides
You can download the presentation slides for this post here:
👉 MindLLM Neuroscience-Informed Attention Slides (.pptx)
🧠 The Core Idea
MindLLM takes raw brain activity (fMRI signals) and transforms it into a set of semantic tokens that can be interpreted by a Large Language Model (LLM) like Vicuna.
It does this by:
- Using learnable queries to extract meaningful patterns
- Defining keys using voxel location + brain region identity
- Using values as raw fMRI activity
Together, this forms a subject-agnostic encoder: it can process any person’s brain scan, regardless of voxel count or brain shape.
🧬 What is Neuroscience-Informed Attention?
It’s an attention mechanism that treats:
- Values as raw fMRI signals
- Keys as spatial and anatomical context
- Queries as learnable vectors that extract meaningful brain-wide features
This allows the model to learn where and what to attend to — across brains.
📐 Architecture Breakdown
Inputs per voxel:
- 3D coordinate:
[x, y, z] - Brain region ID: e.g., “FFA”, “V1”, “PPA”
- BOLD signal: voxel intensity (scalar)
Step-by-step for Two Subjects
| Step | Subject A | Subject B |
|---|---|---|
| Voxel count | 12,000 | 15,000 |
| Activation | 12000 × 1 | 15000 × 1 |
| Coords | 12000 × 3 | 15000 × 3 |
| Region IDs | 12000 × 1 | 15000 × 1 |
1. Key Construction
Each voxel is converted to a key using:
- Its position
- Fourier-encoded spatial features (24D)
- Region embedding (8D)
Input vector: 3D + 24D + 8D = 35D
→ Projected to: 64D key
k_i = W_k \cdot [xyz \,||\, \text{Fourier}(xyz) \,||\, \text{RegionEmb}(r_i)]
🧪 Sample Code
Here’s a simplified implementation in PyTorch:
import torch
import torch.nn as nn
import torch.nn.functional as F
# Positional + region encoding (simplified)
def fourier_encoding(coords, num_freqs=4):
out = [coords]
for i in range(num_freqs):
for fn in [torch.sin, torch.cos]:
out.append(fn((2 ** i) * coords))
return torch.cat(out, dim=-1)
class fMRIEncoder(nn.Module):
def __init__(self, num_queries=16, dim=64, region_dim=8):
super().__init__()
self.queries = nn.Parameter(torch.randn(num_queries, dim))
self.key_proj = nn.Linear(3 + 8 + 24, dim) # coords + region + pos_enc
self.value_proj = nn.Linear(1, dim)
self.output_proj = nn.Linear(num_queries * dim, 128 * num_queries)
def forward(self, voxel_values, coords, region_ids):
# Positional and region encodings
pos_enc = fourier_encoding(coords) # [voxels, 24]
region_embed = nn.Embedding(100, 8)(region_ids) # [voxels, 8]
keys = self.key_proj(torch.cat([coords, pos_enc, region_embed], dim=-1))
values = self.value_proj(voxel_values)
# Attention
attn_scores = self.queries @ keys.T / (keys.shape[-1] ** 0.5)
attn_weights = F.softmax(attn_scores, dim=-1)
z = attn_weights @ values # [num_queries, dim]
return self.output_proj(z.flatten()).reshape(-1, 128) # [num_queries, token_dim]